research

I currently work in numerical linear algebra, high-dimensional statistics, and quantum information. I hope to help develop mathematical foundations of quantum algorithms and contribute to the physics of learning.

Lab for Parallel Numerical Algorithms

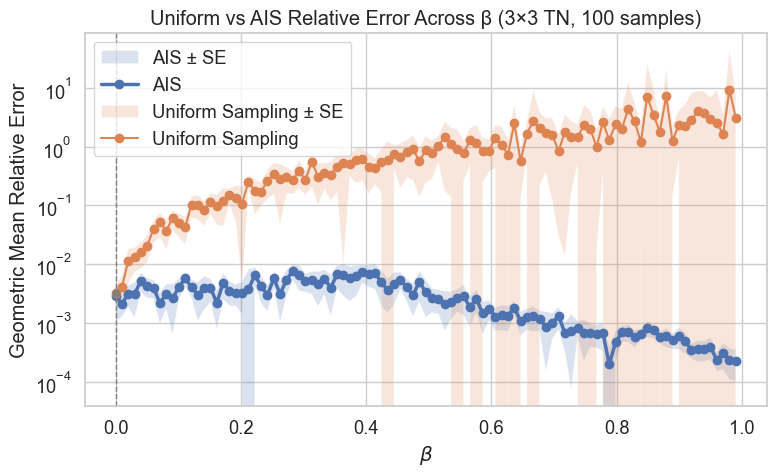
(i) mcmc for tensor network contractions

We are developing a Markov chain Monte Carlo algorithm to estimate contractions of closed tensor networks. This allows efficient approximation of contraction quantities using methods from statistical physics to improve mixing. Such contractions \[ \text{Tr}(ABCD) = \sum_{ijkl} A_{ij}B_{jk}C_{kl}D_{li} \]are trivial in small cases but become \(\#\textsf{P}\)-hard for large networks. Our approach targets use cases in quantum circuits and chemistry, where exact contraction is intractable.

QSim '25 , Read more here!

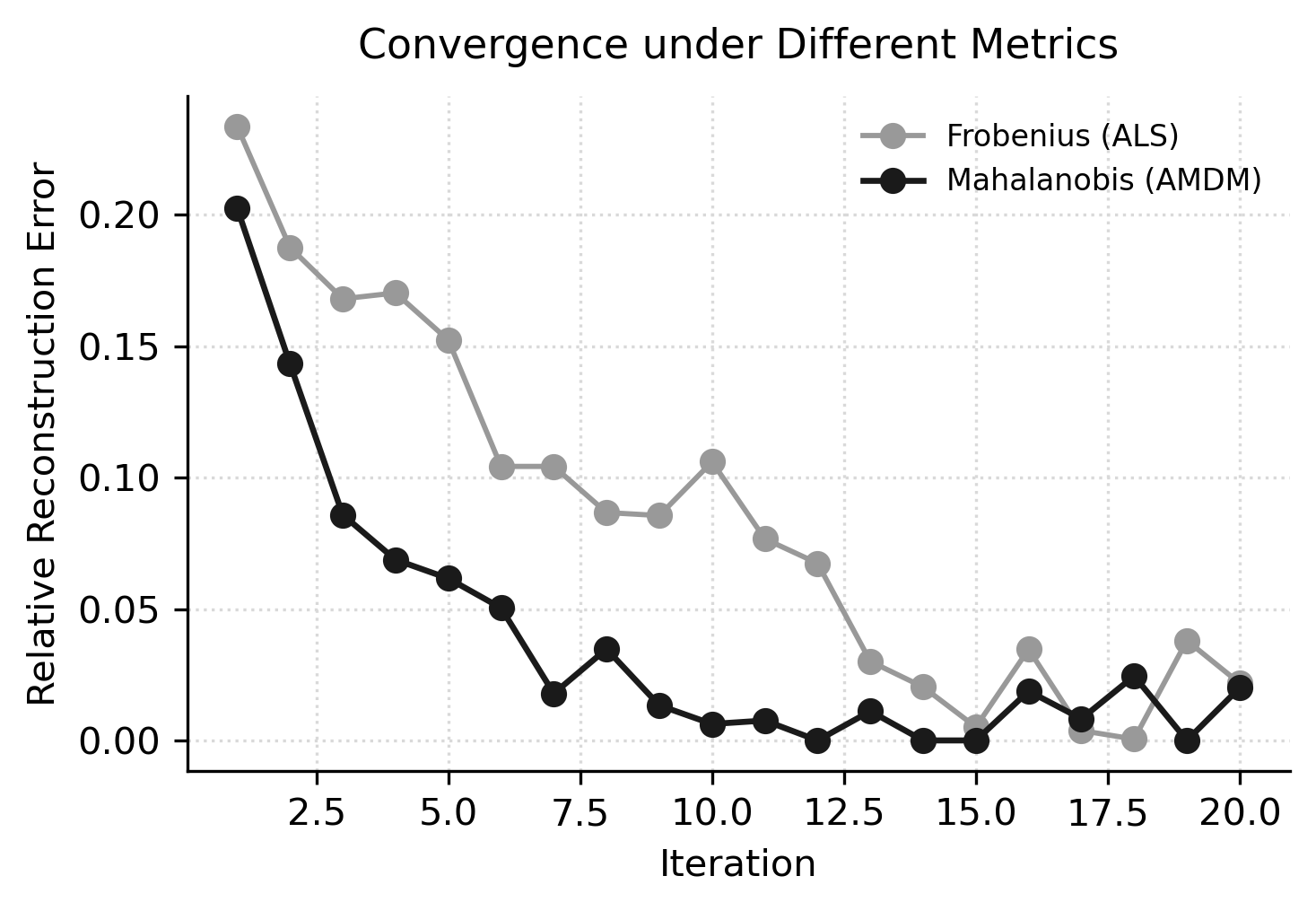
(ii) bayesian tensor decompositions

We are developing Bayesian algorithms for tensor decomposition and probabilistic linear algebra. Currently, we are building on Alternating Mahalanobis Distance Minimization (AMDM) to design a Bayesian tensor decomposition method with mode-wise covariance modeling. By interpreting AMDM as maximum likelihood estimation under a Kronecker-structured Gaussian prior, we aim to create new optimization schemes that combine statistical inference with deterministic tensor solvers for improved conditioning and uncertainty estimation.

More updates soon!